Simplicity and Complexity

Murray Gell-Man was a Nobel laureate who received the award for his theoretical work on elementary particles, especially for coining the term “quark,” alongside a colleague of his. Murray co-founded the Santa Fe Institute, where he was one of the only three professors at the time. In the 90s, he wrote a book titled “The Quark and the Jaguar: Adventures on the Simple & the Complex.”

Simplicity and complexity are, I believe, mostly spoken about from a non-intellectual standpoint. Addressing the implications of both terms is vastly difficult and the reason why we avoid it altogether. To combat this, I found Murray’s ideas provide a good repertoire of tools we can leverage for better understanding both concepts.

Complexity

All systems could be illustrated as compositions of variables. The number of connections within it posits a good proxy for first inferring the complexity underlying the system. Exchanges between nods imply that effects occurring at the microlevel can profoundly alter the whole. If nods learn from past behavior and are in continuous contact with one another, estimating the impact of an input on total output becomes much more difficult.

Figure 3 exhibits a composition of 8 variables, or dots, with increasing levels of communication between them. System A shows no connections whatsoever, whereas all dots in system F have the maximum number of connections.

At a first glance, one tends to think that complexity increases proportionally to the connections per dot. It appears as if A is the simplest of all figures, while F the most complex. But, “is that sensible?”

After more careful analysis, one arrives at the conclusion that, interestingly, both A and F are the simplest. Having no communication at all between variables resembles all variables being connected, at the system level. However, it is very different when there are connections, but these are limited.

Gell-Man believes the most complex figures in the image are C and D. I suspect this realization is reached after trying to understand these compositions of variables. Without omniscient knowledge, one ignores the connections within a system. An analytical struggle follows in two respects. Dots must first be precisely mapped, and a mechanism must be developed to visualize where connections lie. Noticing there are either zero or all connections possible immensely facilitates the analysis. To the contrary, knowing there could be connections between any two dots in a system is daunting. Figuring out which those are is highly complex. And, furthermore, it entails selective connections. Understanding their nature is needed as well.

Algorithmic Information Content

When computers were created, they provided mankind with a new ground for thought. Novel terms and ideas arose. Machines operate in an exquisite fashion. And, by trying to get them to perform a certain task, the mechanisms on which computers function need to be deeply understood.

Computers have historically operated utilizing a binary system of inputs, namely 1s and 0s. When processes need to be carried forward, the strings of data can get indefinitely lengthy. It is therefore crucial to compress the string of data as much as possible.

Compression depends upon the regularity that’s present in a string of bits. If the string is “1111111111,” It can be written as 10 1s. If it is “100100100100,” it can be written as 4 100s. The longer and less obvious the regularity, the more difficult it is to come up with a valid algorithm for compressing the message. Algorithmic Information Content (AIC) refers to the shortest algorithm that can be created for compressing a string of data; it captures the shortest possible description. Finally, a completely irregular string of data presents the highest AIC; there are no patterns and therefore no possible compression.

Complexity, Randomness, and Regularity

Up to a certain point, effective complexity increases as a string of data presents more irregularities. And it peaks when a system is right in between extreme order and disorder. Just like a string of data such as “1111111” is incredibly simple, a completely random string, representing pure disorder, is simple as well. There is no complexity underlying randomness.

Although complexity may be attributed to something difficult to understand, at a deeper level, complexity gives me a sense of organized intelligence. Patterns must be present in any complex system. Their existence reveals either a developed mechanism to combat a certain phenomenon or a standardized method for responding to something that repeats itself.  

Murray pointed out the very peculiar fact that intelligent beings can only evolve in an ecosystem that presents high degrees of irregularity, but not complete. It must have some patterns of regularity so that intelligence can be effectively practiced. Intelligent creatures familiarize themselves with the environment and learn from it, adapting their behavior. In order for this to happen, the context must provide them with opportunities for doing so. A completely regular ecosystem may cause intelligence to be capped as soon as the system is figured out, which occurs promptly. To the contrary, for beings cannot develop any sound practice where randomness abounds, no intelligence can evolve around complete irregularity.

Depth

The second layer upon which complexity can be analyzed is the depth underlying a system. Systems can be fully described utilizing words or strings of bits. Algorithmic complexity refers to how laborious it is to compress the information; meaning how difficult it is to come up with a valid algorithm. Once it is created, we can think of the reverse operation. Depth may be understood as how laborious it is to go from the compressed program to the full-blown description of the system and its regularities.

A great example is Goldbach’s conjecture. In 1742, during the course of an epistolary exchange with a friend, Goldbach proposed that “every even natural number greater than 2 is the sum of two prime numbers.” Although he claims not to have been able to prove it, he was certain about his theorem. Almost 300 years later, the conjecture has not been proven true nor false. It remains unanswered and, seemingly, undecidable.

Goldbach’s conjecture posits a problem whose answer could be searched for by a short program. The program would look for the smallest number g that satisfies both requirements. Although the program itself could be very brief, a computer working on these instructions would take an indefinitely long time before finding g. Therefore, despite g lacking effective complexity and having low AIC, it has extraordinary depth.

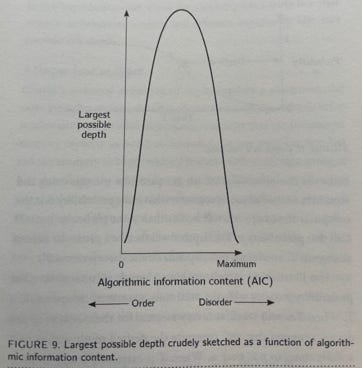
Figure 9 roughly depicts the relation between depth and AIC. If you make a computer execute a program that’s completely regular, like “PRINT one trillion zeroes,” the machine does not have to do much thinking, although printing out the whole string might take time. Where order is at its maximum, the AIC is low, and so is depth. Similarly, if you make the machine print a completely random string, which, by definition, has maximum AIC, the computer doesn’t have to do much thinking either. By this means, one could argue that depth may be at its largest when in between order and disorder.

Note: I’m still dazzled by Goldbach’s conjecture. Seems to go against the chart, but I used it because it very well captures the concept of depth.

Cripticity and Literature

An interesting concept to further think this through is provided by theoretical scientists’ work. Their job roughly matches that of the computer as aforementioned. Theorists are in charge of identifying regularities in systems and coming up with hypotheses, potentially capable of explaining observed phenomena. Crypticity accounts for the opposite of depth. It is a rough measure of how difficult it is the theorists’ job with a certain system.

There’s a famous thought experiment that provides a common ground for many modern critiques. Hypothetically, if we put a set of chimpanzees in front of a typewriter and they are forced to push buttons, obviously randomly, they will eventually type out one of Shakespeare plays, which may hold the highest complexity within literature.

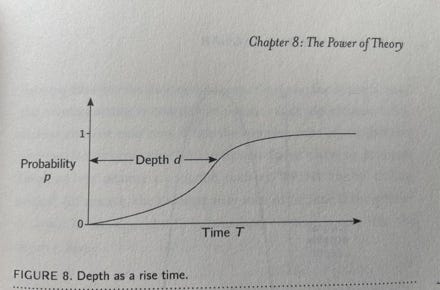
Notwithstanding this, Gell-Man asks us to think about what the probability of such a thing occurring is and how long it would take. Literature offers a very distinctive type of depth. How words relate to one another, composing sentences of the widest form, makes there being incalculable depth within texts. In some sense, thinking about a scale of depth for literature work, it should take more time for chimpanzees to end up writing deeper books. Figure 8 illustrates this example, with probability of the event happening equaling one.

Organic beings exhibit a very similar level of depth. For natural selection has been acting on us all for such a long period of time, the depth embedded in every organism is massive. Recalling the idea of going from the brief program, or end result, to the full description of the system, we’d see how indefinitely long it would be to do this with species.

Final Remarks

Very hard book and really tough concepts to contend with. I remain having not grasped them fully, but hope to have expressed them decently. My sense is that these words/tools/ideas are very useful for inferring a system’s complexity and how to deal with it.